Cryptologie avancée
Ces exercices permettent de découvrir et mettre en application des notions avancées de cryptologie.
La machine Enigma
Prérequis : maîtrise des classes et de l’opérateur modulo, première partie du TP
Culture générale
Tu en as peut-être déjà entendu parler, Enigma est une machine de cryptologie mise au point et utilisée par les allemands pendant la seconde guerre mondiale. Après avoir longtemps été considérée comme incassable, le mathématicien Alan Turing, qui est aujourd’hui considéré comme le père de l’informatique moderne, parvint à comprendre son fonctionnement et fut en mesure de décrypter les messages chiffrés avec Enigma.
Mais comment fonctionne Enigma ?
1. Les rotors
La machine Enigma est composée de 3 parties mobiles appelées “rotors” (visibles sur la photo ci-dessous). Ces rotors associent une lettre de l’alphabet à une autre. Les trois rotors sont connectés les uns aux autres. Imaginons que l’on donne un A au premier rotor, celui-ci pourrait par exemple le transformer en F. Le second rotor transforme le F en O et le troisième transforme le O en E. Note ici que les rotors n’appliquent pas un chiffre de César, si A devient F avec le premier rotor, cela ne veut pas dire que B deviendra G.

Une machine Enigma
En code, on peut représenter un rotor par une chaîne de 26 caractères.
| Alphabet | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
|---|---|
| Rotor 1 | E K M F L G D Q V Z N T O W Y H X U S P A I B R C J |
Ici, on peut comprendre que le rotor 1 donnera E en sortie pour un A en entrée, un K pour un B, etc.
Dernière chose, afin de changer l’état de la machine et de rendre plus complexe le déchiffrement, les rotors peuvent tourner d’un 26ième de tour. Quand cela se produit, les lettres transformées par le rotor changent. Si l’on tourne d’un cran le rotor 1 défini au dessus, le fil dans le rotor qui reliait A à E reliera désormais B à F. De la même manière, le fil qui reliait B à K reliera désormais C à L, etc…
Puisque cela serait trop simple de tourner les 3 rotors à chaque fois, les cryptologues allemands ont mis au point le système suivant : pour chaque lettre tapée, le rotor 1 tourne d’un cran. Le rotor 2 tourne lui d’un cran quand le rotor 1 a fait un tour complet (c’est-à-dire toutes les 26 lettres tapées), et le rotor 3 tourne d’un cran à chaque tour complet du rotor 2 (toutes les 676 lettres tapées).
2. Le réflecteur
Après avoir fait passer la lettre dans les 3 rotors, on la passe dans une pièce appelée le réflecteur. Le réflecteur est une partie similaire à un rotor, car il associe une lettre à une autre, mais reste fixe sans tourner. Enfin, on fini par renvoyer la lettre dans les rotors en sens inverse, et le tour est joué !
3. Le tableau de permutations
Comme si cela n’était pas déjà assez compliqué, on rajoute une couche avec le tableau de permutations. Le fonctionnement de celui-ci est très simple. Il s’agit simplement de brancher des lettres 2 par 2 pour échanger leur place (on peut échanger comme cela jusqu’à 10 paires de lettres). On branche ce tableau avant le système de rotor. Par exemple, si l’on échange les lettres A et O, alors chaque A tapé par l’opérateur de la machine deviendra un O pour le système des rotors, et chaque A “renvoyé” par ce dernier sera un O pour l’opérateur (et vice-versa, le O devient un A).
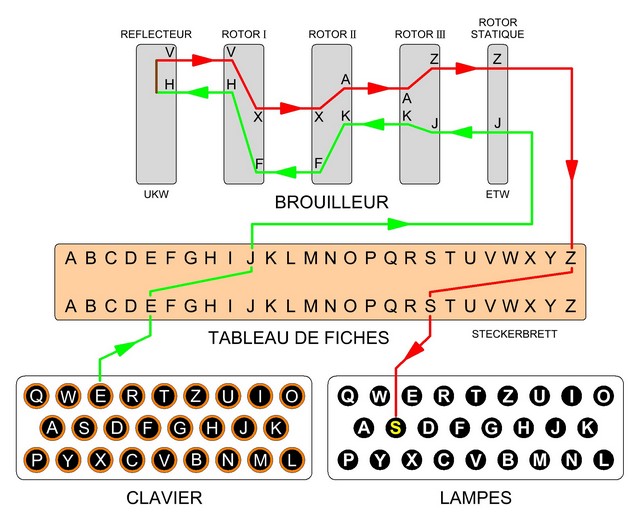
Schéma de fonctionnement d’Enigma
Vous pouvez aussi visualiser le fonctionnement d’Enigma sur ce site : https://observablehq.com/@tmcw/enigma-machine
4. Et pour décoder un message ?
Tu viens d’apprendre le fonctionnement général de la machine Enigma, mais une question persiste : avec un système aussi complexe, comment fait-on pour déchiffrer un message chiffré avec une machine Enigma ? La réponse est sûrement plus simple qu’il n’y paraît : il suffit de taper le message chiffré sur une machine Enigma qui a les mêmes paramètres initiaux que pour chiffrer le message ! En effet, prenons le message “GirlsCanCode” et imaginons que tous les rotors soient sur le cran 0 au début du message. Taper G sur la machine donnera une lettre différente, peut-être un V. Mais de la même manière, si l’on avait tapé V, on aurait obtenu G, car le chemin de la lettre dans la machine est le même, seulement il est parcouru à l’envers.
Exercices
À ton tour de créer ton propre programme Enigma !
Afin d’implémenter notre propre machine Enigma, nous utiliserons une classe qui nous sera utile pour sauvegarder l’état actuel des rotors.
Voici le squelette du code:
|
|
Voici également deux simples fonctions permettant de trouver l’indice d’une lettre dans l’alphabet (en partant de 0), et vice-versa :
|
|
Enfin, voici des rotors et réflecteurs qui ont réellement été utilisés pendant la seconde guerre mondiale :
|
|
Partie 1 : encode_letter
Dans cette méthode de la classe Enigma, tu dois chiffrer la lettre donnée en paramètre.
Entrée :
letter: la lettre à chiffrer
Sortie :
- La lettre chiffrée correspondante
ATTENTION: après avoir trouvé la lettre, il ne faut pas oublier de modifier la position des rotors.
Partie 2 : encode_message
Dans cette méthode, il te faut encoder tout un message avec le programme Enigma !
Entrée :
msg: le message à chiffrer
Sortie :
- Le message chiffré
N’oublie pas que tu peux utiliser la méthode encode_letter dans encode_message.
Fais attention aux caractères spéciaux dans ton message, les chiffres, espaces et caractères de ponctuation ne peuvent pas être chiffrés par Enigma.
Une fois implémenté, tu peux tester ton code de la manière suivante :
|
|
Si tout fonctionne normalement, le programme devrait afficher la version chiffrée puis déchiffrée de ton message !
Partie 3 : Bonus
Bien joué !
Pour aller plus loin, tu peux modifier le programme pour ajouter la fonctionnalité du tableau de permutation, qui n’est pas montrée ici.
Info: une particularité de la machine Enigma qui a aidé Alan Turing et son équipe pour casser le code est la suivante : Enigma ne donnait jamais de lettre identique à celle donnée en entrée. Saurais-tu expliquer pourquoi ?
XOR / Ou Exclusif
Prérequis : l’hexadécimal, la table ASCII
Quelques rappels : le binaire
Le binaire est un système permettant d’écrire des nombres en utilisant 2 symboles : 0 et 1.
À titre d’exemple, voici comment compter de 0 à 10 en binaire :
| Nombre | Binaire |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
L’hexadécimal
L’hexadécimal est un système permettant d’écrire des nombres en utilisant 16 symboles : les chiffres de 0 à 9 (inclus), puis les lettres de A à F (inclus).
À titre d’exemple, voici comment compter de 0 à 20 en hexadécimal :
|
|
Remarque : on utilise le système décimal, en base 10, dans la vie courante. Il utilise donc 10 symboles : les chiffres de 0 à 9.
Un peu de théorie
Le XOR est un opérateur logique, on l’appelle également le OU Exclusif et en anglais eXclusive OR. Il est souvent représenté avec le symbole : “$\oplus$”. En Python, on utilisera le caractère ^.
Table de vérité :
- On définit $A$ et $B$ deux opérandes binaires sur lesquelles on va appliquer XOR.
| $A$ | $B$ | $A \oplus B$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
En observant la table de vérité, on peut dire que le XOR peut se définir de la façon suivante :
- Si les deux opérandes sont différentes, alors le résultat est 1
- Si les deux opérandes sont identiques, alors le résultat est 0
Chiffrer des messages avec XOR
Dans cet exercice, vous allez chiffrer des messages avec XOR. Cet opérateur logique possède en effet des propriétés intéressantes qui vont permettre de chiffrer et déchiffrer un message avec la même clé.
Pour mieux vous faire comprendre le processus, appliquons-le avec un exemple en binaire. Admettons que le message que l’on souhaite chiffrer est 01100101 01110000 01101001 et que la clé est 01110100 01100001 01100001.
|
|
Cette explication avait pour but de vous faire comprendre le fonctionnement de XOR et du processus de chiffrement / déchiffrement. Lorsque vous allez coder cette méthode de chiffrement en Python, vous n’aurez pas besoin de passer par du binaire, vous utiliserez de l’hexadécimal.
Maintenant que vous connaissez le XOR, il est temps d’écrire les fonctions !
Let’s code
Pour implémenter cette méthode de chiffrement, il va être plus simple de diviser le problème en plusieurs parties, et donc en plusieurs fonctions. Comme écrit précedemment, pour appliquer le XOR, pas besoin de passer par du binaire, nous allons utiliser de l’hexadécimal. La première fonction va donc transformer du texte en hexadécimal. La deuxième va appliquer XOR sur le message transformé en hexadecimal avec une clé en hexadecimal de la même longueur. Finalement, la troisième va transformer de l’hexadecimal en lettres, texte lisible pour nous !
Comment obtenir une clé en hexadécimal de la même longueur que le message que l’on souhaite chiffrer ?
C’est tout simple, une fonction générant des clés en hexadécimal vous est fournie : randomHexa(lenstr). Elle prend en paramètre lenstr qui correspond à la longueur du message initial en lettres et renvoie une clé générée aléatoirement. Cette fonction vous sera grandement utile pour effectuer vos tests !
Voici la fonction :
|
|
Elle utilise une fonction que vous devez implémenter. En cas de difficulté, n’hésitez pas à demander de l’aide :)
Exemple d’application :
|
|
Ainsi, il va falloir implémenter les fonctions stringToHexa(s), msgXor(m, key) et hexaToString(hexa).
La fonction stringToHexa(s)
Cette fonction va se charger de transformer une chaîne de caractères formée de lettres en une chaîne de caractères en hexadécimal. Elle prend en paramètre s, une chaîne de caractères.
Pour convertir une chaîne de caractères en hexadécimal. Il va falloir le faire lettre par lettre et appliquer quelques transformations à chacune des lettres :
- Calculer la valeur de la lettre dans la table ASCII (nombre entier)
- Convertir la valeur ASCII en sa représentation hexadécimale (chaîne de caractères)
- Adapter le résultat de l’étape précédente pour qu’il soit de longueur 2 (ajouter des 0 si besoin) et qu’il ne contienne que de l’hexadecimal (sans “0x”, voir la fonction
hex()expliquée plus bas)
Quelques fonctions utiles !
|
|
La fonction msgXor(m, key)
Cette fonction va se charger d’appliquer XOR entre le message et la clé (soit message ⊕ clé). Elle prend donc en paramètre m une chaîne de caractères correspondant au message que l’on désire chiffrer, et qui a déjà été converti en hexadecimal. Elle prend également key qui est également une chaîne de caractères en hexadecimal et qui est de la même longueur que m. msgXor(m, key) va renvoyer une chaîne de caractères en hexadecimal.
Pour appliquer XOR, voici les différentes étapes qu’il faudra implémenter :
- Sélectionner chaque caractère des chaînes de caractère 2 par 2
- Les convertir en nombre entier
- Appliquer XOR !
Quelques fonctions utiles…
|
|
La fonction hexaToString(hexa)
Cette fonction va se charger de convertir une chaîne de caractères de valeurs hexadécimales, en une chaîne de caractères de lettres, que l’on pourra lire et comprendre. Elle va donc renvoyer une chaîne de caractères. hexaToString(hexa) prend en paramètre hexa, une chaîne de caractères en hexadécimal.
Les fonctions dont vous aurez besoin pour implémenter votre solution ont déjà été expliquées plus haut. Les étapes ne sont pas données mais vous pouvez les déduire des étapes de stringToHexa().
À vous de jouer !